On the day of Ramanujan’s return back to India from Cambridge, Hardy, a rather famous mathematician of the 20th century and a mentor and friend to Ramanujan, mockingly blamed his “rather dull” taxi-cab number, which was 1729, for him being late at the port. Proving Littlewood true, yet again, who said, “Every integer is like one of Ramanujan’s personal best friends,” Ramanujan replied, which came out almost naturally, “No Hardy, it is a very interesting number. It is the smallest number expressible as the sum of two cubes in two different ways.”

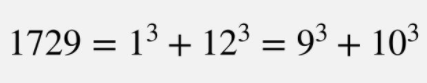
While I am not sure how or when 1729 came under the mathematical limelight is it known by almost all mathematics enthusiasts for this peculiar property. However, 1729 has some other really cool properties as well, which are not very heard of.
Harshad Number:

A Harshad number, which was first classified by Indian recreational mathematician, Dr. Kaprekar (1905–1986). Harshad number are also known as Niven numbers (or multi digital numbers), most commonly in Java, which is as Dr. Ivan Niven delivered a paper at a conference in Number theory talking about the Harshad numbers in 1977.
Harshad numbers have a peculiar yet fun property, they can be divided by the sum of their own digits. In other words, they leave a remainder of 0 when divided by the sum of their own digits. The mathematical expression for this is:
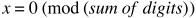
Now, 1729 happens to be a Harshad number, too! Let’s see how: For 1729, the sum of its digits is = 1 + 7 + 2 + 9 = 19. If you divide 1729 with 19, you get a quotient of 91 and a remainder of 0! Voila!
If you observe closely, there is another cool pattern here, 91 is like the mirror image of 19 or 19 written in reverse! That way, 1729 can also be said to be the divisible by the sum of its digits and its reverse!
Carmichael number:
Here, again we are exposed to Fermat’s Little theorem, wonderful how Fermat pops up almost everywhere! Let’s have a look at a test that is applied to check if a number is prime or not and we are going to use Fermat’s little theorem. It says if you have a number, ‘a,’ and you raise it to the power of a number, ‘n,’ and you subtract the original number, ‘a,’ again and this resultant is divisible by n, p has to be be a prime! The mathematical expression for it is:
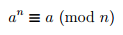
However, later it was observed that this theorem had some exceptions. Like if you consider 341 as n and 2 as a, it holds true, thereby implying 341 is a prime number
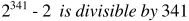
But when you perform the same with a = 3, it does not hold, thereby implying 341 is not a prime and is composite! So, what is the truth? It turns out, 341 is composite and can be expressed as the product of 11 and 31! Here 2, which gave off a false impression of 341 being a prime, is called a Fermat’s liar number and 3 which corrected our previous assumption of 341 being a prime is called a Fermat’s witness. But, you might wonder, can there be composite numbers that pass every such test for all values of a? Yes, these are called the Carmichael number!
Korselt was the first who observed the basic properties of Carmichael numbers, but he did not give any examples. In 1910, Carmichael found the first and smallest such number, 561, which explains the name “Carmichael number”. Following which other numbers popped up as well, lets look at the first six Carmichael numbers

Wait wait, do you see it? 1729 happens to be the third Carmichael number!
Euler Pseudoprime:
An odd composite integer n is called an Euler pseudoprime to base a, if a and n are co-prime, and
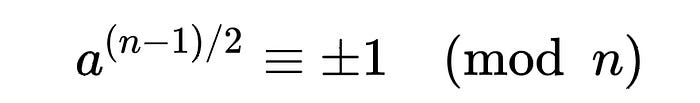
The motivation behind this originates from the fact that every prime number n satisfies the above equation, deduced from the little theorem, which says that if n is prime, and co-prime to a, then a^n−1 ≡ 1 (mod n). Suppose that. n > 2 is prime, then n can be expressed as 2m + 1 where m is an integer. Thus, a.(2.m + 1) − 1 ≡ 1 (mod n), which means that a ^ (2.m − 1) ≡ 0 (mod p). This can be factored as (a.m − 1)(a.m + 1) ≡ 0 (mod n), which is equivalent to a^(n−1)/2 ≡ ±1 (mod n).
Euler pseudoprime are also Fermat pseudoprimes. It is not possible to produce a definite test of primality based on whether a number is an Euler pseudoprime because there exist absolute Euler pseudoprimes, numbers which are Euler pseudoprimes to every base relatively prime to themselves. The absolute Euler pseudoprimes are a subset of the absolute Fermat pseudoprimes, or Carmichael numbers, and the smallest absolute Euler pseudoprime is 1729 = 7×13×19!
Sphenic Number:
A sphenic number is any number that can be expressed as the product of three prime numbers. 1729, too is a sphenic number, as 1729 can be expressed as the product of 7, 13, and 19, all of which are primes!
Zeisel number:
Zeisel number, probably first introduced by Kevin Brown, while he was looking for numbers that when plugged into 2^{k-1}+k yielded prime numbers. Later 1885 was pointed out to be such a number by Helmut Zeisel. Soon it was discovered that 1885 has prime factors that follow:
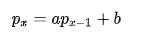
Finding more and more numbers that followed the above equation led onto naming them as Zeisel numbers, defined asa square-free integer k with at least three prime factors which fall into the given pattern, where a and b are some integer constants and x is the index number of each prime factor in the factorisation, sorted from lowest to highest.
The first few Zeisel numbers are
105, 1419, 1729, 1885, 4505, 5719, 15387, 24211, 25085, 27559, 31929, 54205, 59081, 114985, 207177, 208681, 233569, 287979, 294409, 336611, 353977, 448585, 507579, 982513, 1012121, 1073305, 1242709, 1485609, 2089257, 2263811, 2953711, …
If you have not spotted already, 1729 is the 3rd smallest Zeisel number, with the constants a = 1 and b = 6, its factors being 7, 13 and 19, falling into the pattern:
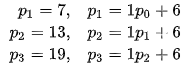
Loeschian number:
Numbers that can be expressed in the form x^2 + x.y + y^2 for integer x, y are called the Loeschian numbers. 1729 is the smallest number that can be expressed as the loeschian number in four different ways, where (x,y) can be: (25,23), (32,15), (37,8) and (40,3).
Galactic Algorithm:
Named after Richard Lipton and Ken Regan, a galactic algorithm outperforms all algorithms for sufficiently large (VERY large) problems. Galactic algorithms have never used for terrestrial data as it is suitable for very large ones.
A very common example of a galactic algorithm is the fastest known way to multiply two numbers and the Fourier transform that it depends on is based on the 1729th dimension. However, it will only reach such high computational speeds when the data if of 2172912 bits or more (at least 101038 digits), which is vastly larger than the number of atoms in the known universe and hence is never used in practice.
It does not end here, 1729 has multiple other applications in real life as well, like it is a centered cube number as well as a dodecagonal number, a 24-gonal[10] and 84-gonal number and has many other properties as well! Isn’t is wonderful the number of ideas and concepts hidden behind a mere taxi-cab number, maybe you’ll be the one to find the next “1729”!
Thank you so much for reading! Constructive criticism is appreciated : )
