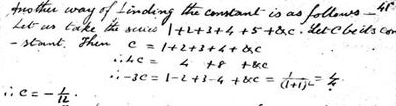
Srinivas Iyengar Ramanujan was an Indian self taught genius, and was probably the only one of his kind. Scribbling, crossing, erasing, he spent most of his childhood in the alcoves of the Narasimha swamy Temple. His devotion to mathematics was such, it was often told that he loved numbers more than people. While he discovered a new theorem almost every day or perhaps even hour, he claimed Namagiri, the goddess he devoted, to appear in his dreams and let know of the theorems. Nonetheless, his genius could never be questioned. Ramanujan, like most other men of such intellect, passed away at a mere age of thirty after having discovered 2000 new theorems in his last living year, which are now stored in the three volumes, called, “Ramanujan’s lost notebook” in the libraries of Cambridge University.
While most of Ramanujan’s work hovered beyond the intellect of most people, he is the most well known among children, and adults, for his seemingly (and in real) unrealistic proof to a negative result to the sum of all natural numbers till ∞.


A -1/12 also happens to pop up in string theory (not the one by Hawking but in the first theory, Bosonic string theory) which happens to explain our world to quite an extent! But could this be real? I mean, it definitely does not make sense, right! Well, don’t believe it? check out Mark Dodd’s article on the actual proof that Ramanujan himself presented for this seemingly unrealistic equation.
Ramanujan started with two series, #T = 1–2+3–4+5–6+7-… & S = 1–1+1–1+1-…
First considering the second equation
S = 1–1+1–1+1-…
Next, he did a little trick,
S = 1-(1–1+1–1+1-…)
If you look closely, the thing inside the brackets is nothing but S itself!
S = 1-S
2S = 1
S = 1/2 — — — — [1]
Rearranging, we land onto the result that the series equals 1/2!
Moving onto the first equation,
T = 1–2+3–4+5–6+7-…
Now we sum two T’s together,
2T = (1–2+3–4+5–6+7-…) + (1–2+3–4+5–6+7-…)
Here, we take 1 out from one of the brackets, just another of Ramanujan’s billion tricks, you’ll get used to it, don’t worry!
2T = 1 + (-2+3–4+5–6+7-…) + (1–2+3–4+5–6+7-…)
Rearranging, we get
2T = 1 + [ (-2+1)+(3–2)+(-4+3)+…]
See where we’re headed?
2T = 1 + [-1+1–1+1-…]
2T = 1–1+1–1+1-…
2T = S = 1/2
T = 1/4
Wonderful, isn’t it?
Now, taking the sum of all integers as U = 1+2+3+4+…, we subtract T from U,
U-T = [1+2+3+..]-[1–2+3–4+…]
U-T = [(1–1) + (2-(-2)) + (3–3) + (4-(-4))+…
Adding, we get,
U-T = 4 + 8+ 12 + …
Again rearranging we get,
U-T = 4 (1+2+3+…) = 4U
U-4U = T
3U = T
As we have already found T = 1/4
3U = -1/4
U = -1/12
Thus, 1+2+3+… = -1/12, but is it actually?
The answer is no! The reason to why the solution to this is wrong comes from one of the most elementary concepts from real analysis, convergence. If you have not already noticed, the first equation that we talked of, S, is nothing but Grandi’s Series.
S = 1–1+1–1+1-…
S can have two possible values, 0, when we consider the sum of even number of terms, & 1 when we consider the sum of odd number of terms, but S as a whole doesn’t have any particular solution as it neither considers the sum of even nor odd number of terms, but an infinite number of terms. You may ask why Grandi’s series doesn’t have a solution when many other infinite series do, the answer to this will lead us to why Ramanujan’s infinite series is false.
But before we begin, lets write S in a summation form to give it a more “mathy” and compact look,
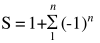
If we were to look at the values that we get from S as we vary n from 1 to ∞, the values would jump to and fro between 0 and 1, or in other words, the value of S does not “converge” towards anything!
To get out heads around the idea of convergence, lets consider a simpler function,
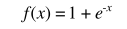
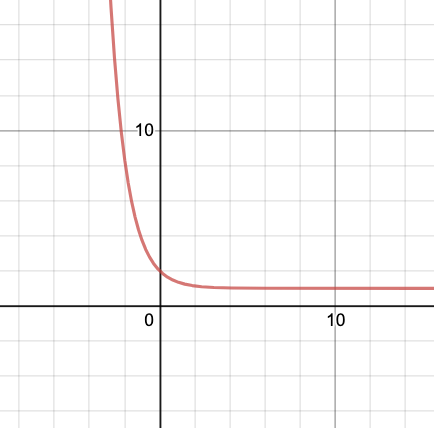
As evident from the plotted graph, as the value of x is increased, the function, f(x) slowly tends to 1 as the graph turns flat. Or we can say, the function converges to 1.
While on the other hand, a function like,
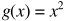
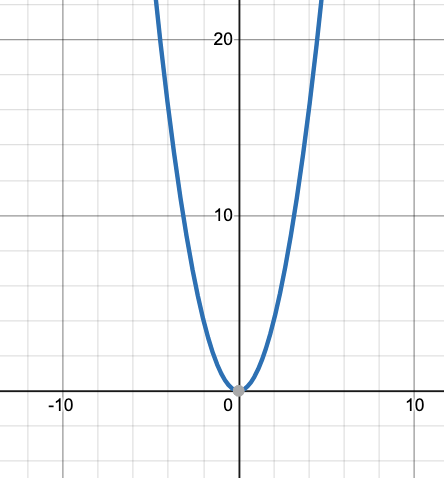
is not converging, as, as we increase the value of x, the function g(x) tends to ∞ unlike f(x) that converged to a constant 1.
The key reason behind Ramanujan’s infinite series being wrong is the consideration that S equals 1/2, which in a real case scenario is impossible, even though it was proven to equal 1/2 with clever mathematical manipulations as S is not converging, i.e, even when we take the sum of infinite terms of S, we would either get 0 or 1 and adding further terms would lead to the same result, 0 or 1. Here S is an alternating series, i.e for sum of odd number of terms we get a particular result, here 1, and for the sum of even number of terms we get another result, here 0, and the values keep zig-zagging.
A similar mistake can also be spotted for the second series, T.
T = 1–2+3–4+5–6+7-…
Rearranging and simplifying we get,
T = (1–2)+(3–4)+(5–6)+…
T = -1–1–1–…
Or in more mathematical terms,
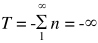
Its disaccord with the initially found value of 1/4 is justified as we had used S = 1/2 to find the same, and as we have already seen, S = 1/2 is an absolutely wrong statement.
Moreover, U, which is the sum of all natural numbers can be written as,

As evident from the expression of U in terms of limits, n(n+1)/2 cannot be simplified to get a result anything other than ∞. Thus as the sum of all natural numbers, n(n+1)/2, is in no way convergent, we cannot expect it to converge to -1/12 but rather would go up to ∞.
It is interesting to note the occurrence of a -1/12 in string theory as discussed earlier, however, it deserves an article of its own. The same would be released within a week as a part of this series on Ramanujan’s works.
