A series on world’s shortest mathematics papers, pt.2: Niven’s half page paper on the irrationality of π.
Irrational numbers are funny, the decimal digits go on and on but the entire number is always less than a fixed value, isn’t it awkward? What seems even more astonishing is how such numbers are related to every circle, drawn on a plane, out there in the world! Yes, π is what I am talking about. Here we will talk about a half page proof to the irrationality of this awkward number, π.


The human civilisation has known of π and its relation to the perimeter and areas of circles for millennia; evidence dates the knowledge of π in the human civilisation to the ancient babylonians when the last mammoths got extinct! However, while the estimated value of π went from 3 to 3.12 to 3.14 and so on, the nature of its irrationality was only discovered and proved by Johann Heinrich Lambert — (German: [ˈlambɛʁt], Jean-Henri Lambert in French; 26 or 28 August 1728–25 September 1777) — a Swiss polymath in 1760, and later by other prominent mathematicians like Hermite, Cartwright, Bourbaki and Laczkovich.
However, while most of these proofs considered high levels of mathematics, a paper by Dr. Ivan Niven does the job with easy and simple to understand tools condensed in a half page paper by the good old method of contradiction. Let’s see how.
First consider π to be a rational number, which can be expressed as π = a/b where a&b are integers and b≠0. And lets also consider a function:

Where we can vary the n from 1 to any number n to create a polynomial, F(x):

Now, going back to f(x), it is evident that when n! is multiplied with f(x), the denominator comes out to be 1 and hence the resultant f(x) value for any x is an integer. So,

Now, if you consider the right hand side, the lowest power of x in (a -b.x)^n is 0, in term a^n, and when this is multiplied by x^n, the lowest power of x in the resultant is n and the highest is n+n = 2n.
If you differentiate f(x), the resultant will always be 0 for when x = 0 or (a — b.x) = 0 => x = a/b = π (as considered earlier) as all terms in the numerator have x in them. Now, lets differentiate {F’(x) sin x — F(x) cos x} with respect to x.

I’ll leave differentiating this as a fun and easy activity for you. After a little simplification we get as a result:

As you might know, integration is the inverse of differentiation and vice versa. Thus if we integrate f(x) sin x, which is what we got after differentiating {F’(x) sin x — F(x) cos x}, we should get {F’(x) sin x — F(x) cos x} as a result! Integrating the same under the limits 0 to π, we get:

Here, π = a/b. As we have already talked of before, F(π) + F(0) is an integer as differentiating f(x) any number of times we get integers as results for x = a/b = π and x = 0.
But as f(x) is a polynomial function, for 0 < x < π, the minimum value of f (x). sin x, is 0 while the value of x for which f(x). sin x = 0 is maximum can be found by differentiating it, following which if the value is substituted, we get an upper bound on the value of this function in the above mentioned limit.
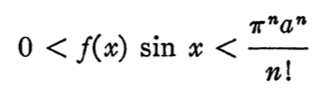
Nice, so the integral is positive, but it would not actually hold for a very large value of n as the constant or the upper bound tends to 0 for larger values of n.

Or in other words the integration that should have been valid for any value of n breaks at larger values of n. So, there are two things that could have gone wrong, either there was a mistake in the integration procedure or π cannot actually be written as a/b. But if you’d verify the integration procedure by multiple methods, the result is always the same, leaving just one option or π ≠ a/b or π is irrational!
Though there are now many who have memorised thousands of digits of π but it is only few that know a way to prove its irrationality. Though there are many proofs, even one by Bourbaki, a French mathematician who never existed, to π’s irrationality, the proof by Ivan Niven happens to be the most concise. Taking it as granted takes away all the fun and enjoyment math has to offer. π’s irrationality, the proof by Ivan Niven happens to be the most concise!